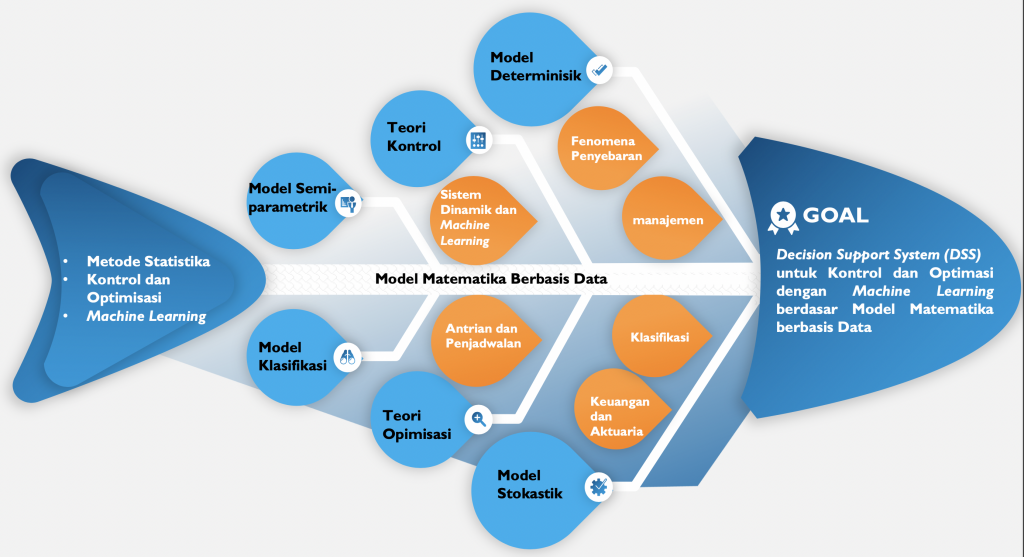
Mathematics as the mother of all sciences can be used to explain quantitatively the phenomena in everyday life which are represented by a mathematical model. In general, there are two types of mathematical models, namely the deterministic model and the stochastic model. The deterministic model is a model that does not contain randomness in the sense that if the initial conditions are known, the conditions at each subsequent time can also be known through the model. The advantage of this deterministic model is the ease of doing the analysis, while the drawback is that it only explains the phenomena on an average basis. The stochastic model pays attention to the element of randomness, which means that even though the initial conditions are known, the conditions at subsequent times cannot be determined clearly. Of course, the drawback of this stochastic model is the level of complexity that is quite high, but the advantage is the ability to explain the uncertainty of a phenomenon by using the concept of probability.

Various mathematical models have been developed by researchers and some are used to support decision making (Decision Support System; DSS). Several models that have been developed include disease spread models, smoking behavior spread models, queuing models, scheduling models, assignment models, transportation route optimization models, stock price prediction models, classification models, and various other models. Mathematically, these models are represented by systems of differential equations, Markov processes, linear programming, non-linear programming, regression, time series, and so on.

Mathematical models that are formed certainly contain parameters that must be estimated from data or observations. Estimation of these parameters is facilitated by using several statistical methods. Broadly speaking, there are three approaches, namely parametric, non-parametric, and semi-parametric. All three have their own characteristics including their use based on the context of the application and the nature of the data.

Control theory provides facilities for conducting quantitative analysis of how a phenomenon changes. On the other hand, optimization theory provides a method for finding the optimal value of an objective in a problem. The combination of the two can be used to carry out a quantitative analysis of changes made to the system represented by a mathematical model so that a goal is achieved optimally. An example is how to conduct a quantitative analysis of a policy so that the goals of decision-makers are achieved optimally. Another example is how to define many service tables so that the queue is not too long but the resources used are not too much.

As technology develops, especially in the field of Artificial Intelligence (AI), mathematical research certainly needs to integrate and optimize AI. Although the mathematical model is constructed based on real phenomena, it requires assumptions to transform real problems into mathematical language. Therefore, the results of the model analysis including the control and optimization cannot be interpreted and used directly on this phenomenon. However, the interpretation of the results of the mathematical modeling can be used as a reference by policymakers in making decisions. The main problem now is the lack of a comprehensive decision support system (DSS) starting from the construction of mathematical models, parameter estimation, control and optimization, interpretation, and use of the photographed phenomena. Furthermore, mathematical models that integrate machine learning are still very limited.

The big picture of my research is the problem-based mathematical models supported by statistical methods and machine learning. Some of the areas that I have explored are the phenomenon of the spread of disease, the spread of smoking behavior, queuing, scheduling, and classification models.